고정 소수점 & 부동 소수점

실수의 표현 방식

• 컴퓨터가 실수를 표현하려면 사람들이 일반적으로 사용하는 10진수가 아니고 기계어인 2진수 표현 방식을 사용한다.
• 하지만 실수를 2진법으로만 표현하기 어렵기 때문에 여러 가지 방법들이 연구되었고 지금 주로 사용하는 방법은 2가지다.
  1. 고정 소수점(Fixed Point) 방식
  2. 부동 소수점(Floating Point) 방식

이진기수법

고정 소수법과 부동 소수점을 설명하기 앞서 2진법 변환 방법을 설명하도록 하려고 한다.

1. 10진수에서 2진수로 변환

먼저 사진의 예를 들면 35라는 숫자를 2진법으로 변환하는 예시이다.

10진수에서 2진수로 변환하는 방법은 2진법으로 변환하려는 수를 몫이 1이 될 때까지 계속 2로 나눈다.

그리고 몫부터 시작해서 나머지를 거슬러 올라가면서 표기를 한 후 그 뒤에 2진법이라는 것을 알 수 있게 (2)를 붙여준다.

1. 35를 2로 나누면 몫은 17이 나오고 나머지는 1이 나온다.
2. 17을 2로 나누면 몫은 8이고 나머지는 1이 나온다.
3. 8을 2로 나누면 몫은 4이고 나머지는 0이 나온다.
4. 4를 2로 나누면 몫은 2이고 나머지는 0이 나온다.
5. 2를 2로 나누면 몫은 1이고 나머지는 0이 나온다.
6. 몫이 1이 되었기 때문에 나눗셈을 중지하고 몫부터 나머지까지 거슬러 올라가면서 표기한다.
7. 몫부터 거슬러 올라가면 100011로 표기되고 2진법 표시인 (2)를 붙여준다.
8. 100011(2)

2. 2진수에서 10진수로 변환

위에서 계산한 100011(2)을 다시 10진수로 변환하는 방법을 소개하려고 한다.

2진수를 10진수로 변환하는 방법은 맨 뒤자리수는 2의 0제곱 즉 1이고 점점 올라가게 된다.

2의 0제곱 2의 1제곱 2의 2제곱 이런 식으로 올라가게 된다.

그리고 1로 되어있는 자리만 곱셈을 하고 각각 더하면 10진수가 완성된다.

1. 100011(2)에서 맨 뒤부터 살펴봤을 때 맨 뒤자리는 2의 0제곱이고 1 * 1 = 1이 된다.
2. 그 다음으로 넘어갔을 때 2의 1제곱 자리이므로 2 * 1 = 2가 된다.
3. 그 다음 2의 2제곱 자리는 0이기 때문에 계산하지 않는다.
4. 2의 3제곱 자리도 0이기 때문에 계산하지 않는다.
5. 2의 4제곱 자리도 0이기 때문에 계산하지 않는다.
6. 2의 5제곱 자리는 1이므로 32 * 1 = 32이 된다.
7. 곱셈 계산이 끝났고 각 자리에 있는 수를 더하면 32 + 2 + 1이므로 더하면 35가 나오게 된다.

고정 소수점(Fixed Point) 방식

그림의 고정 소수점 방식을 보면 앞의 16비트는 부호와 정수부를 뒤의 16비트는 소수부를 나타내는 것을 볼 수 있다.

고정 소수점 방식은 정수부와 소수부의 자릿수가 크지 않으므로, 표현할 수 있는 범위가 매우 적다는 단점이 있다.

즉 소수점의 위치를 고정시켜 표현하는 방식이고 크고 정밀한 실수를 표현하지 못하기 때문에 컴퓨터에서는 사용되지 않는다.

부동 소수점(Floatin Point) 방식

• 고정 소수점은 정수부와 실수부를 나누어서 나타냈지만 부동 소수점은 가수부와 지수부로 나누어 표현하는 방식을 사용한다.

• 고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작지만 부동소수점은 소수점의 위치를 고정하지 않기 때문에 매우 큰 실수까지 표현할 수 있다.

• 부동소수점 수식

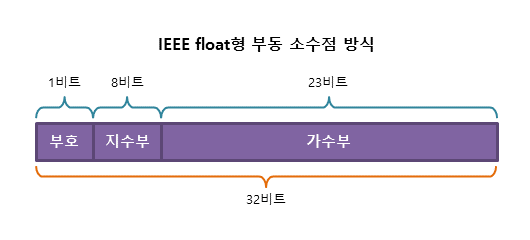
• ±(1.가수부)×2^(지수부-127)

• 32비트 float형 실수에서 IEEE 부동 소수점 표현 방식

  

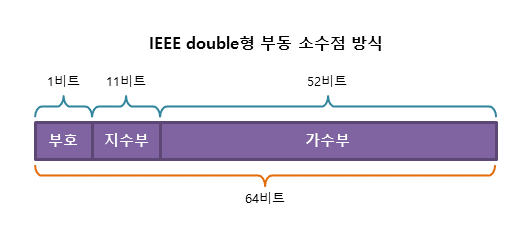
• 64비트 double형 실수에서 IEEE 부동 소수점 표현 방식

  

부동 소수점 방식의 오차

부동 소수점 방식의 공식을 사용하게 되면 표현할 수 있는 범위는 늘어나지만, 10진수를 정확하게 표현할 수는 없게 된다.

따라서 컴퓨터에서 실수를 표현하는 방법은 정확한 표현이 아닌 언제나 근사치를 표현할 뿐임을 항상 명심해야 한다.

val result = 0.0
for (i 0 until 1000) {
    result += 0.1
}
println("0.1을 1000번 더한 합계는 ${result}입니다."

실행결과
0.1을 1000번 더한 합계는 99.999입니다.

위의 예시 코드의 실행결과를 보면 100이 아닌 99.999가 출력되는 것을 확인할 수 있고 실수 연산을 수행할 때는 오차가 발생함을 알 수 있다.

면접 예상 질문

고정 소수점이란 무엇인가?

부동 소수점이란 무엇인가?

컴퓨터에서 0.1을 1000번 더했을 때 나오는 값은 무엇인가?