퀵 정렬

퀵 정렬(quick sort)

개념

분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법

• 합병 정렬(merge sort)과 달리 퀵 정렬은 리스트를 비균등하게 분할한다

정렬 과정

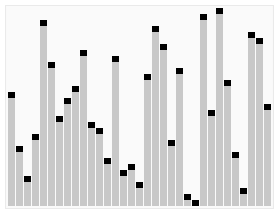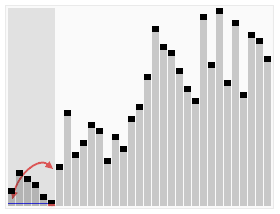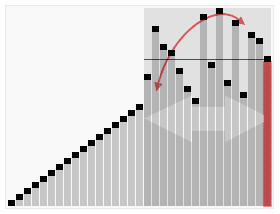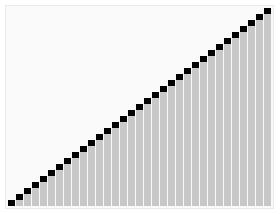
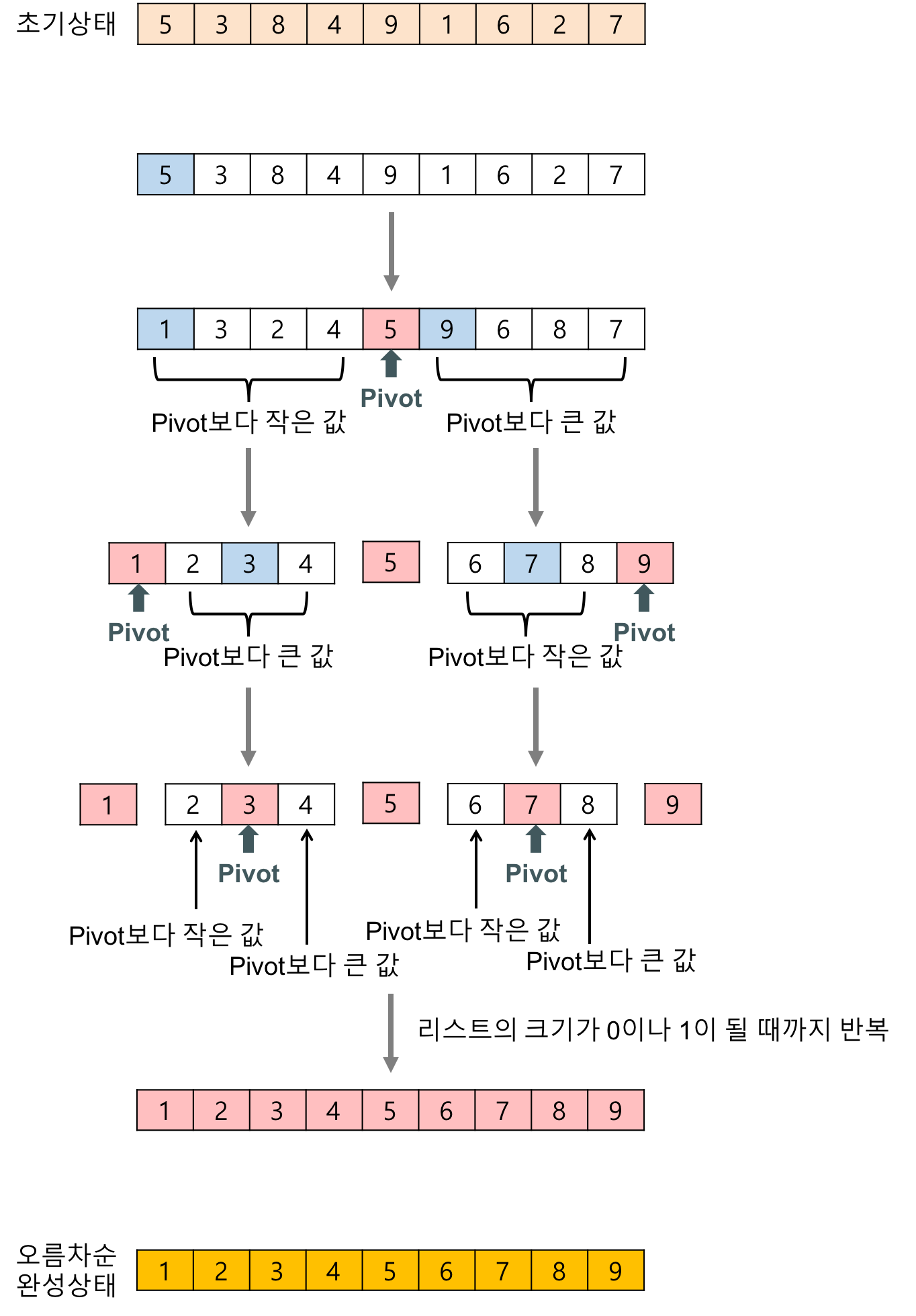
1. 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
2. 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
   (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
3. 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
   - 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
   - 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
4. 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
   - 리스트의 크기가 0이나 1이 될 때까지 반복한다.

예제 코드 (코틀린)

fun partition(arr: IntArray, left: Int, right: Int): Int {
    var low = left + 1
    var high = right
    val pivot = arr[left]
    var done = false

    while (!done) {
        while (low <= high && arr[low] <= pivot) low++
        while (low <= high && arr[high] >= pivot) high--
        if (high < low) {
            done = true
        } else {
            val tmp = arr[low]
            arr[low] = arr[high]
            arr[high] = tmp
        }
    }

    val tmp = arr[high]
    arr[high] = arr[left]
    arr[left] = tmp

    return high
}

fun quickSort(arr: IntArray, left: Int, right: Int) {
    if (left < right) {
        val pivotIndex = partition(arr, left, right)

        quickSort(arr, left, pivotIndex - 1)
        quickSort(arr, pivotIndex + 1, right)
    }
}

fun main() {
    val arr = intArrayOf(5, 3, 8, 4, 9, 1, 6, 2, 7)

    quickSort(arr, 0, arr.size - 1)

    arr.forEach {
        print("$it ")
    }
}

예제

💡 배열에 5, 3, 8, 4, 9, 1, 6, 2, 7이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해보자

퀵 정렬에서 피벗을 기준으로 두 개의 리스트로 나누는 과정
(코틀린 코드의 partition 함수의 내용)

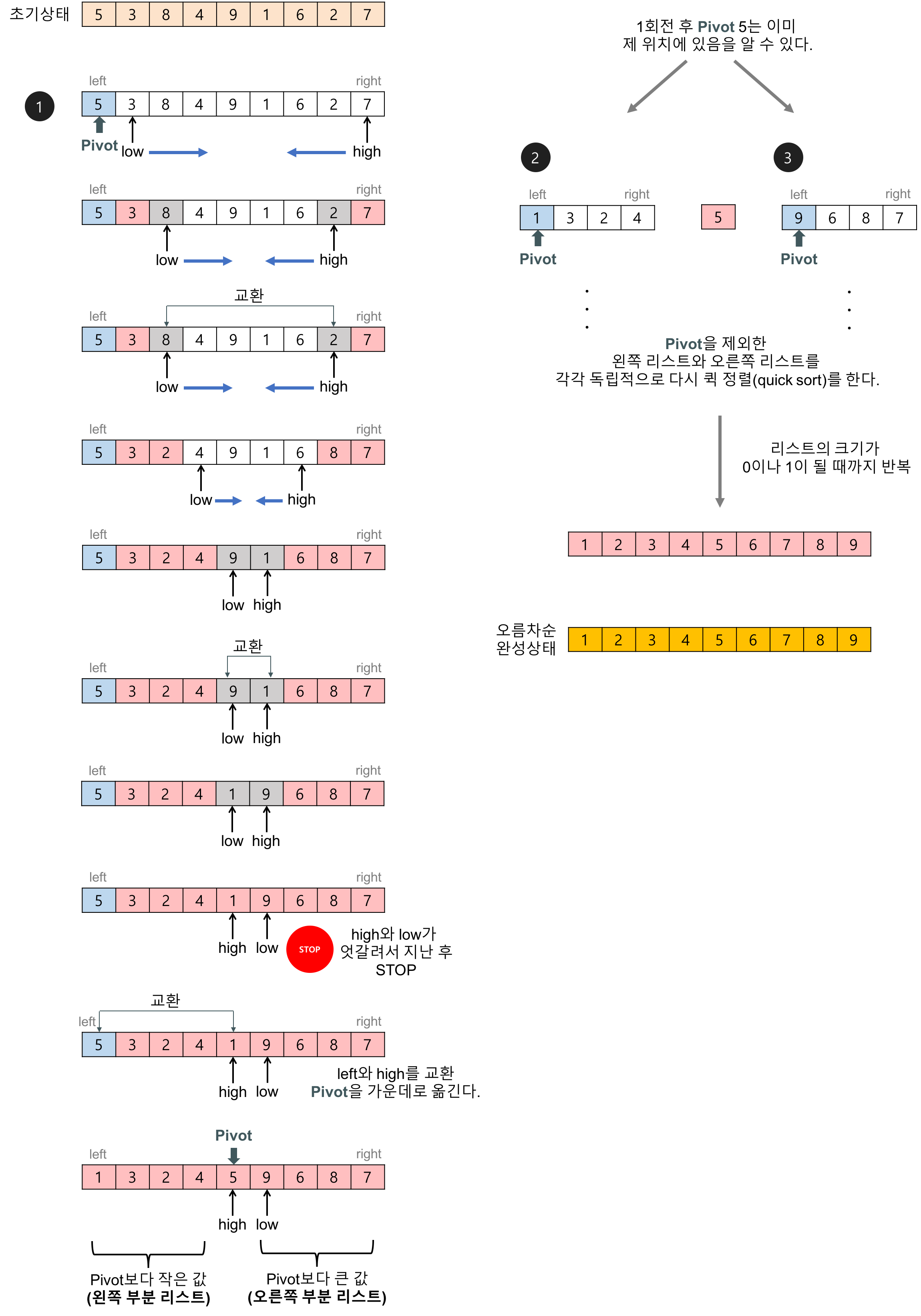
피벗 값을 입력 리스트의 첫 번째 데이터로 하자. (다른 임의의 값이어도 상관없다.)
2개의 인덱스 변수(low, high)를 이용해서 리스트를 두 개의 부분 리스트로 나눈다.

1회전: 피벗이 5인 경우,

1. low는 왼쪽에서 오른쪽으로 탐색해가다가 피벗보다 큰 데이터(8)을 찾으면 멈춘다.
2. high는 오른쪽에서 왼쪽으로 탐색해가다가 피벗보다 작은 데이터(2)를 찾으면 멈춘다.
3. low와 high가 가리키는 두 데이터를 서로 교환한다.
4. 이 탐색-교환 과정은 low와 high가 엇갈릴 때까지 반복한다.
5. left(피벗)와 high가 가리키는 두 데이터를 서로 교환한다.

2회전: 피벗(1회전의 왼쪽 부분리스트의 첫 번째 데이터)이 1인 경우,

• 위와 동일한 방법으로 반복한다.

3회전: 피벗(1회전의 오른쪽 부분리스트의 첫 번째 데이터)이 9인 경우,

• 위와 동일한 방법으로 반복한다.

시간 복잡도

최선의 경우

리스트가 계속 딱딱 반씩 나누어지는 경우 (피벗이 중간값일 때)

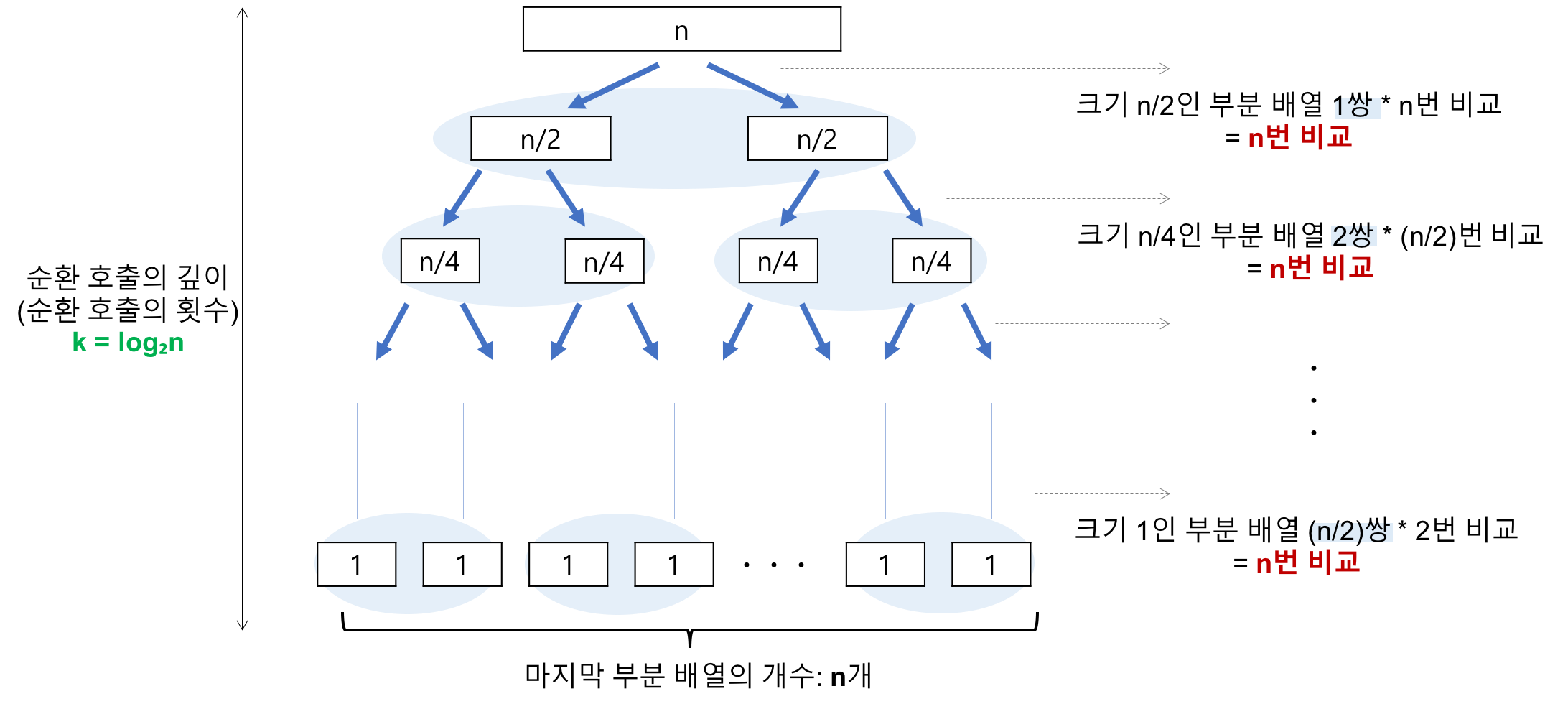
O(nlog(2)n)

최악의 경우

리스트가 계속 불균형하게 나누어지는 경우 (피벗이 리스트의 최대 or 최솟 값일 때)

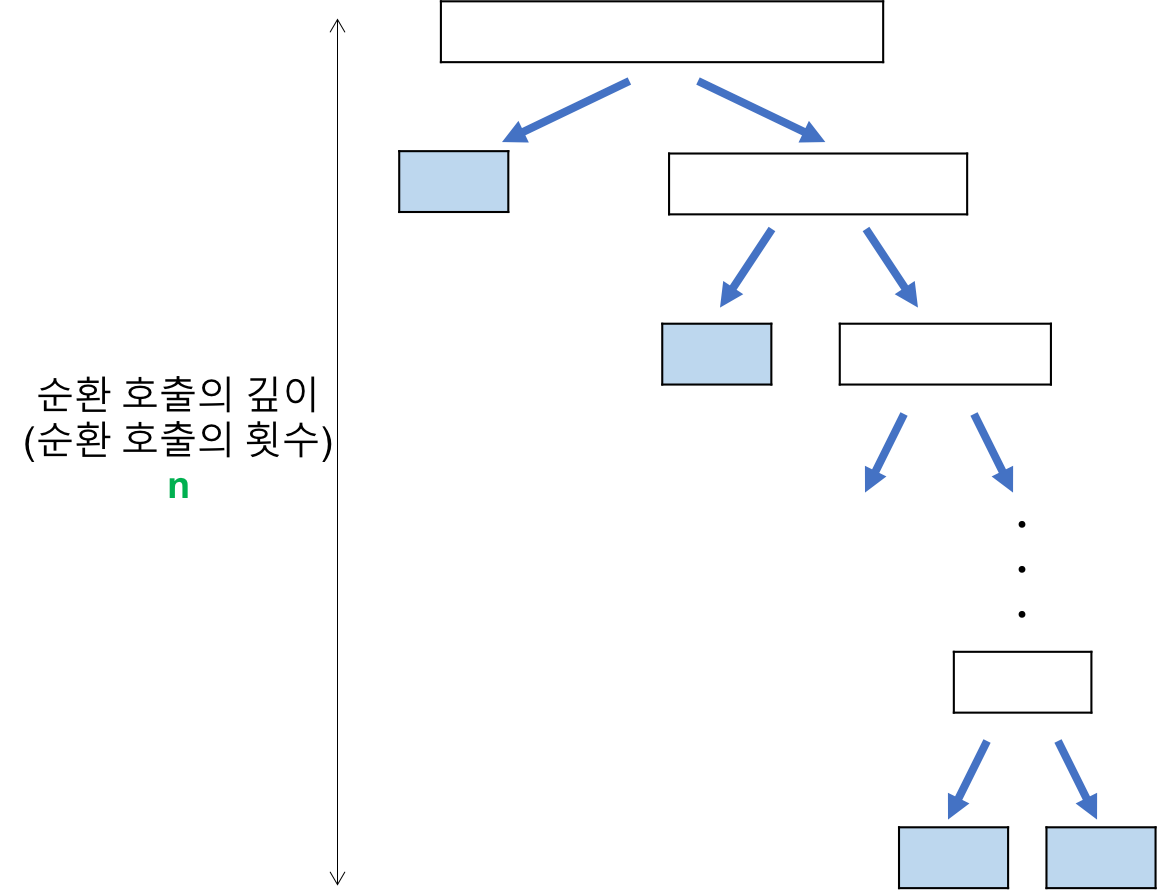
O(n^2)

특징

장점

• 속도가 빠르다

단점

• 불안정 정렬 : 중복된 값이 있을 때 요소의 순서가 바뀔 수 있다
• 정렬된 리스트에 대해서는 퀵 정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다

면접 질문

• 퀵 정렬에 대해 설명해주세요.
• 퀵 정렬이 최악의 시간복잡도를 가지는 경우를 제시해보세요.

참고 URL

https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html

https://notbusyperson.tistory.com/35#article-4--4--퀵-정렬-quick-sort

https://mfamcs.netlify.app/docs/algorithms/퀵 정렬