버블 정렬(bubble sort)
개념
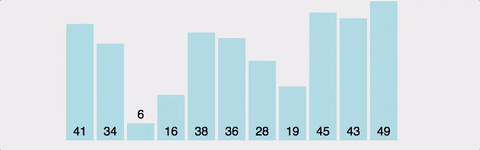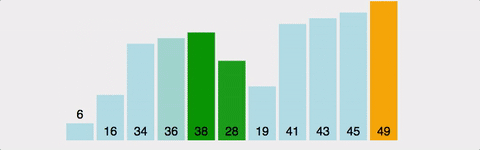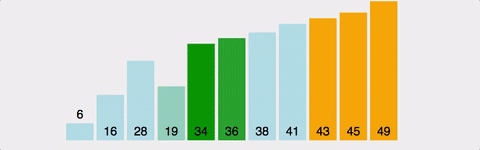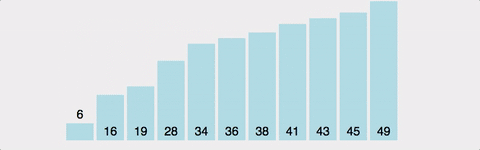
서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정렬하는 알고리즘
정렬 과정
- 1회전에 첫 번째 원소와 두 번째 원소를, 두 번째 원소와 세 번째 원소를, 세 번째 원소와 네 번째 원소를, … 이런 식으로 (마지막-1)번째 원소와 마지막 원소를 비교하여 조건에 맞지 않는다면 서로 교환한다.
- 1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 원소까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
예제
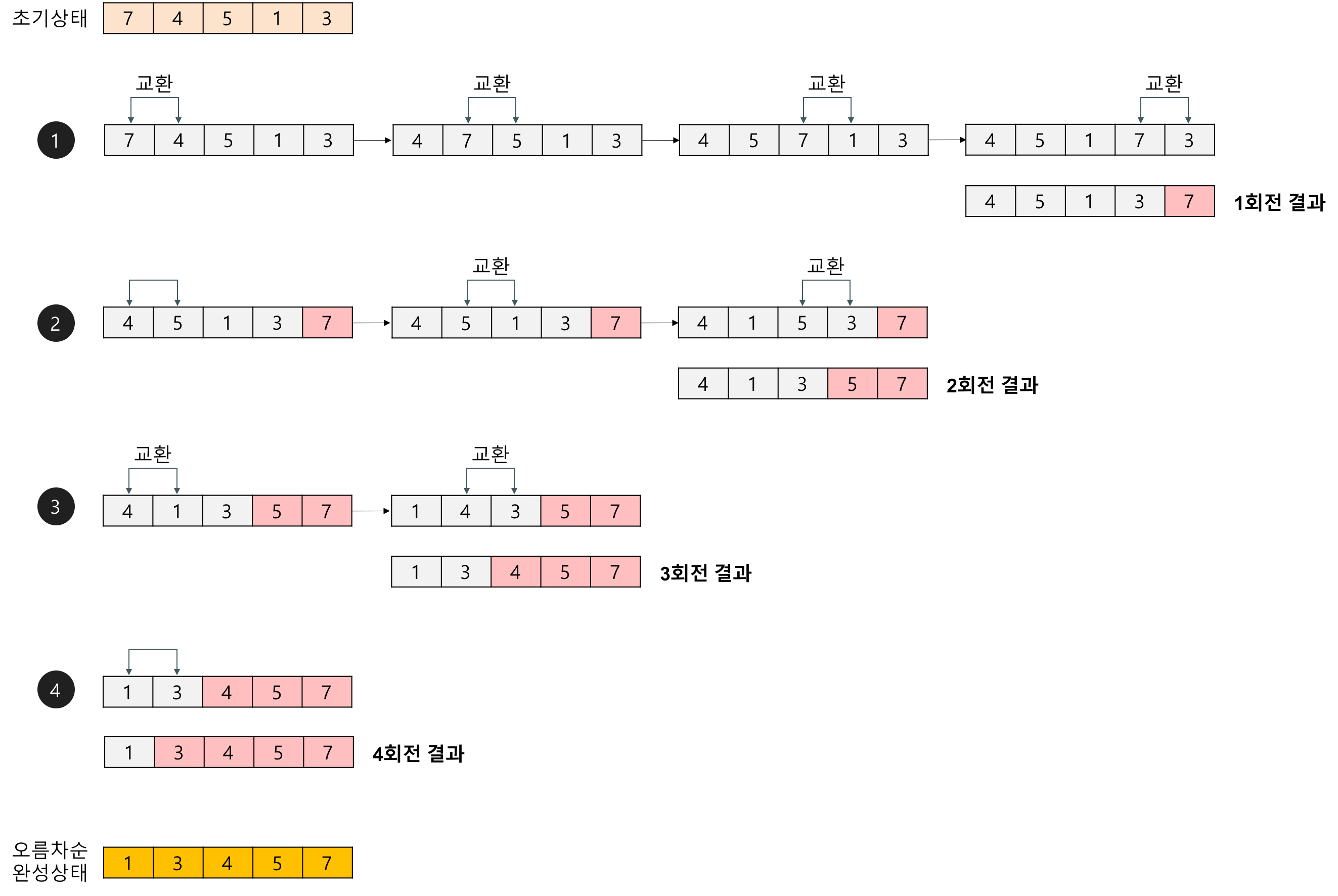
💡 배열에 7, 4, 5, 1, 3이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자
1회전
- 첫 번째 자료 7을 두 번째 자료 4와 비교하여 교환하고, 두 번째의 7과 세 번째의 5를 비교하여 교환하고, 세 번째의 7과 네 번째의 1을 비교하여 교환하고, 네 번째의 7과 다섯 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 네 번 비교한다. 그리고 가장 큰 자료가 맨 끝으로 이동하므로 다음 회전에서는 맨 끝에 있는 자료는 비교할 필요가 없다.
2회전
- 첫 번째의 4을 두 번째 5와 비교하여 교환하지 않고, 두 번째의 5와 세 번째의 1을 비교하여 교환하고, 세 번째의 5와 네 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 세 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 두 번째에 놓인다.
3회전
- 첫 번째의 4를 두 번째 1과 비교하여 교환하고, 두 번째의 4와 세 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 두 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 세 번째에 놓인다.
4회전
- 첫 번째의 1과 두 번째의 3을 비교하여 교환하지 않는다.
예제 코드 (코틀린)
fun bubbleSort(arr: IntArray) {
// i : 최댓값을 고정할 자리의 인덱스
for (i in arr.size - 1 downTo 1) {
// j번째와 j+1번째의 요소가 크기 순이 아니면 교환
for (j in 0 until i) {
if (arr[j] > arr[j + 1]) {
val tmp = arr[j]
arr[j] = arr[j + 1]
arr[j + 1] = tmp
}
}
}
// 출력
arr.forEach {
print(it)
}
}
시간복잡도
데이터가 n개일 때,
1회전에서의 비교 횟수 : 1 ~ n-1 ⇒ n-1개
2회전에서의 비교 횟수 : 1 ~ n-2 ⇒ n-2개
(n-1) + (n-2) + (n-3) + (n-4) +... + 3 + 2+ 1 = n(n-1)/2 => O(n^2)
- 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일하다
- 정렬이 되어있던 안되어있던, 2개의 원소를 비교하기 때문
공간복잡도
데이터가 n개일 때,
주어진 배열 안에서 교환을 통하여 정렬이 되므로,
O(n)
성능 개선 방법과 예제 코드 (코틀린)
단계별로 정렬을 진행 중,
만약 교체가 발생하지 않았다면 정렬이 완료된 것으로 간주하고 멈춘다
fun bubbleSort(arr: IntArray) {
// i : 최댓값을 고정할 자리의 인덱스
for (i in arr.size - 1 downTo 1) {
var quit = true
// j번째와 j+1번째의 요소가 크기 순이 아니면 교환
for (j in 0 until i) {
if (arr[j] > arr[j + 1]) {
val tmp = arr[j]
arr[j] = arr[j + 1]
arr[j + 1] = tmp
quit = false
}
}
// 만약 교체가 발생하지 않았다면 정렬이 완료된 것으로 간주하고 멈춘다
if(quit) break
}
// 출력
arr.forEach {
print(it)
}
}
특징
- 일반적으로 자료의 교환 작업이 자료의 이동 작업보다 더 복잡하기 때문에 버블 정렬은 단순성에도 불구하고 거의 쓰이지 않는다
장점
- 구현이 매우 간단하고, 소스 코드가 직관적이다
- 제자리 정렬(in-place sorting) 알고리즘 : 주어진 배열 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
- 안정 정렬: 비교할 두 값이 같으면 교환을 진행하지 않기 때문에 순서가 바뀔 일이 없다
단점
- 시간복잡도가 최선, 평균, 최악 모두 O(n^2)으로, 굉장히 비효율적이다
- 하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열에서 모든 다른 요소들과 교환되어야 한다
- 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어난다
면접 예상 질문
- 버블 정렬에 대해 설명해주세요
- 버블 정렬 성능 개선 방법에 대해 설명해주세요
참고 URL
https://mfamcs.netlify.app/docs/algorithms/%EA%B1%B0%ED%92%88%20%EC%A0%95%EB%A0%AC
https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html