합병 정렬

합병 정렬(merge sort)

 

 

개념

분할 정복 방식을 이용해서 하나의 리스트를 두 개의 리스트로 분할한 다음 각각의 분할된 리스트를 정렬한 후에 합해서 정렬된 하나의 리스트로 만드는 정렬 알고리즘

 

정렬 과정

분할 단계

1. 주어진 배열의 중간 인덱스를 구한다.
2. 중간 인덱스를 기준으로 배열을 반토막 낸다.

정복 단계

1. 반복해서 반토막을 내다가 마침내 배열의 크기가 0이나 1이 된다.
2. 그러면 주어진 배열을 바로 '답'으로 반환한다.

합병 단계

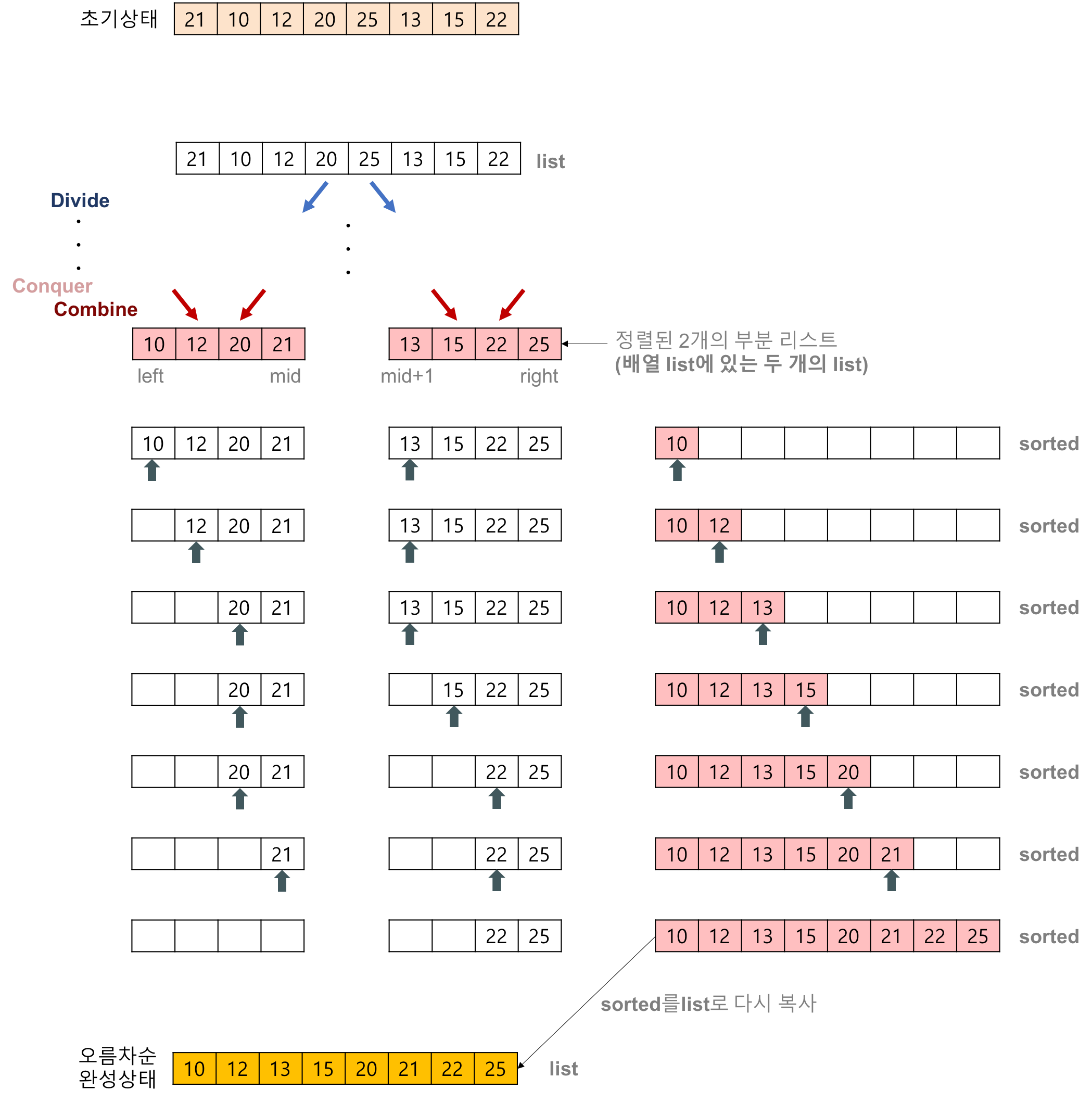
1. 왼쪽 배열, 오른쪽 배열을 인자로 넣어서 각각 정렬된 결과를 얻는다.
2. 양쪽 배열의 맨 앞을 비교해 더 작은 수를 찾는다.
3. 더 작은 수를 꺼내서 새로운 배열에 집어넣는다.
4. 새로운 배열에 모든 숫자가 들어갈 때까지 반복한다.

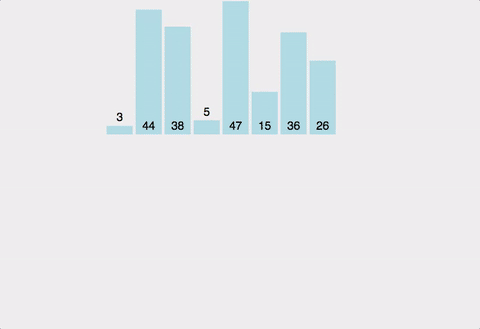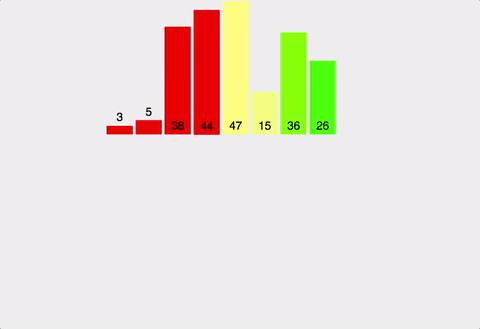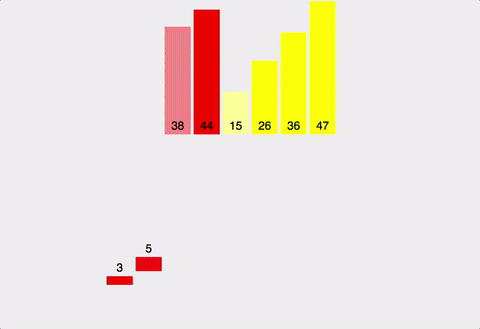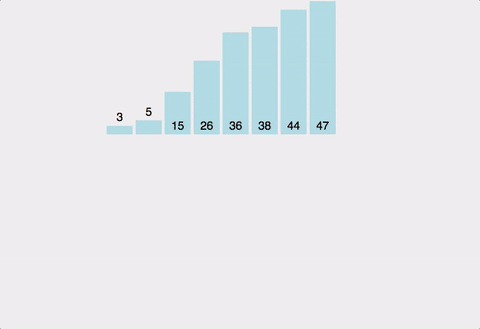
예제

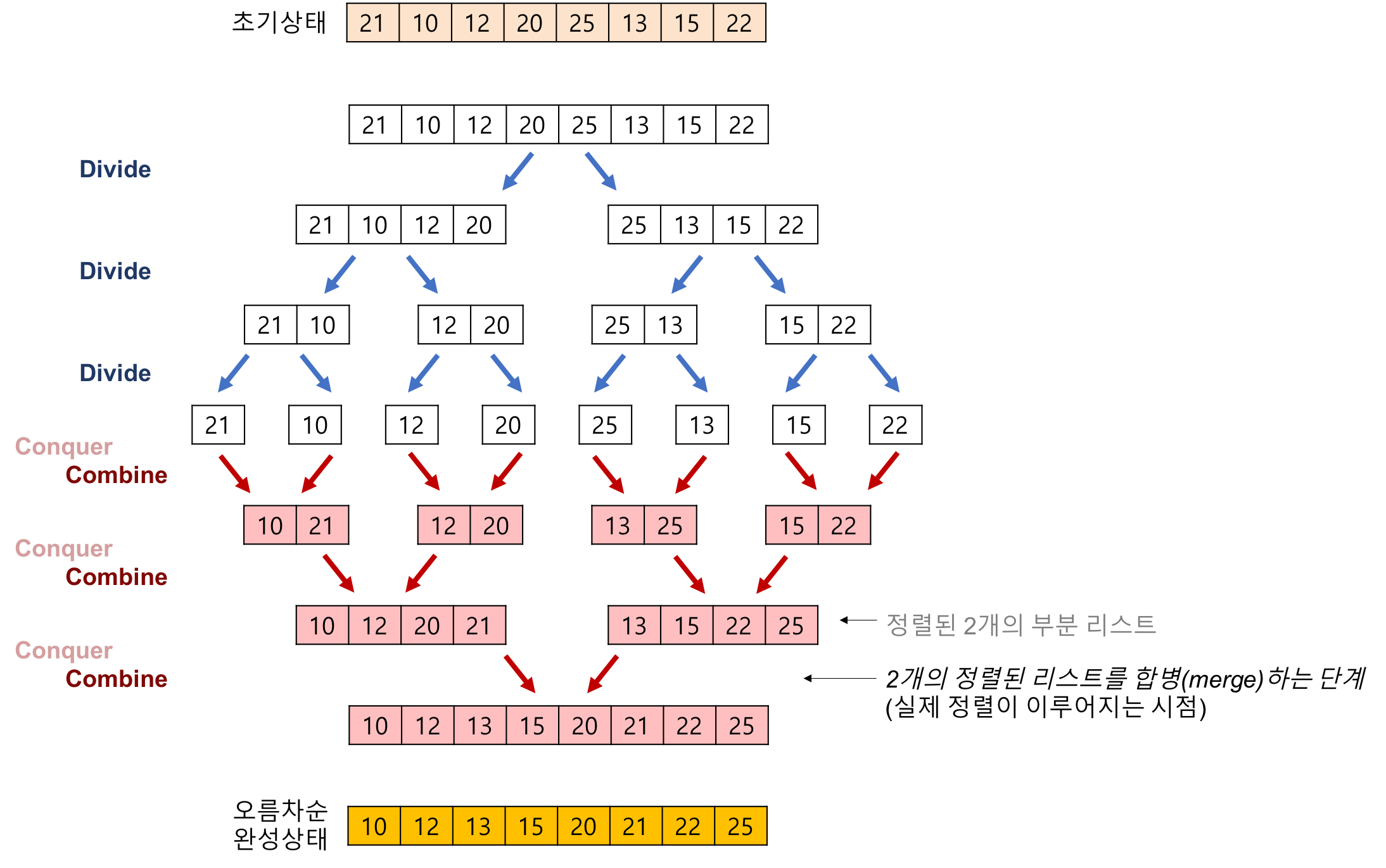
합병 단계 예제

 

예제 코드 (코틀린)

const val size = 8 // 배열의 크기
val tmp = IntArray(size) // 정렬된 배열을 저장할 임시 배열

/* 2개의 인접한 배열 arr[left..mid]와 arr[mid+1..right]의 합병 과정 */
fun merge(arr: IntArray, left: Int, right: Int) {
    val mid = (left + right) / 2 // 중간 위치 계산
    var leftIdx = left // 정렬된 왼쪽 배열에 대한 인덱스
    var rightIdx = mid + 1 //정렬된 오른쪽 배열에 대한 인덱스
    var tmpIdx = left //정렬될 배열에 대한 인덱스

    // 분할 정렬된 배열의 합병
    while (leftIdx <= mid && rightIdx <= right) {
        tmp[tmpIdx++] =
            if (arr[leftIdx] <= arr[rightIdx]) {
                arr[leftIdx++]
            } else {
                arr[rightIdx++]
            }
    }

    // 남아있는 값들을 일괄 복사
    if (leftIdx > mid) {
        for (i in rightIdx..right) {
            tmp[tmpIdx++] = arr[i]
        }
    } else {
        for (i in leftIdx..mid) {
            tmp[tmpIdx++] = arr[i]
        }
    }

    // tmp(정렬된 배열)을 arr로 복사
    for (i in left..right) {
        arr[i] = tmp[i]
    }
}

// 합병 정렬
// 재귀 함수
fun mergeSort(arr: IntArray, left: Int, right: Int) {
    // 재귀 함수 종료 조건
    if (left == right) return

    val mid = (left + right) / 2 // 중간 위치 계산
    mergeSort(arr, left, mid) // 앞쪽 부분 배열 정렬 (자기 자신 호출)
    mergeSort(arr, mid + 1, right) // 뒤쪽 부분 배열 정렬 (자기 자신 호출)
    merge(arr, left, right) // 정렬된 2개의 부분 배열을 합병하는 과정
}

fun main() {
    val arr = intArrayOf(21, 10, 12, 20, 25, 13, 15, 22)

    // 합병 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 7)
    mergeSort(arr, 0, size - 1)

    // 출력
    arr.forEach {
        print("$it ")
    }
}

시간복잡도

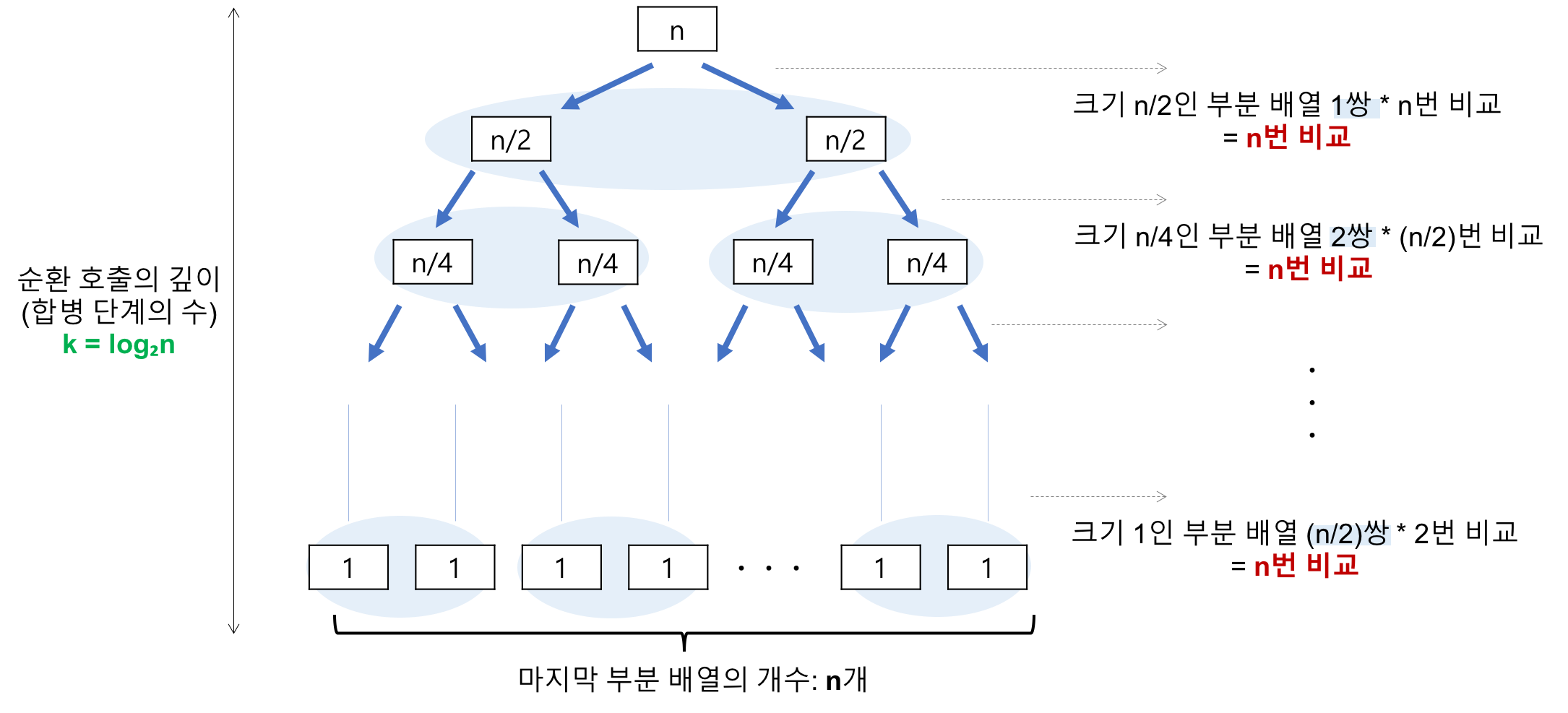
분할 단계

• 비교 연산과 이동 연산이 수행되지 않는다

합병 단계

• 합병 단계의 수 (순환 호출의 깊이)
  • 데이터의 개수 n 이 2의 거듭제곱이라고 가정할 때 n=8의 경우 8->4->2->1 순으로 줄어들어 단계가 3임을 알 수 있다.
  • 이것을 일반화 하면 n=2^k의 경우, k=log(2)n임을 알 수 있다.
• 각 합병 단계의 비교 연산
  • 크기 1인 부분 배열 2개를 합병하는데 최대 2번의 비교 연산이 필요하고, 부분 배열의 쌍이 4개 이므로 2*4=8번의 비교 연산이 필요하다.
  • 다음 단계에서는 크기 2인 부분 배열 2개를 합병하는 데 최대 4번의 비교 연산이 필요하고, 부분 배열의 쌍이 2개이므로 4*2=8번의 비교 연산이 필요하다.
  • 마지막 단계에서는 크기 4인 부분 배열 2개를 합병하는 데는 최대 8번의 비교 연산이 필요하고, 부분 배열의 쌍이 1개이므로 8*1=8번의 비교 연산이 필요하다.
  • 이것을 일반화하면 하나의 합병 단계에서는 최대 n번의 비교 연산을 수행함을 알 수 있다.
• 따라서 합병 단계의 수 * 각 합병 단계의 비교 연산 = nlogn ⇒ O(nlogn)

O(nlogn)

공간복잡도

합병 단계에서 정렬된 숫자들을 저장할 배열을 생성해야 한다.
정렬할 배열과 같은 크기(n)의 새로운 배열이 필요하므로,

O(2n)

 

특징

장점

• 안정 정렬 : 정렬 전 동일한 키 값의 요소 순서가 정렬 후 유지가 되는 정렬 알고리즘
• 입력 데이터가 무엇이든 시간복잡도는 O(nlogn)이다
  • 항상 동일한 시간이 소요되므로 어떤 경우에도 좋은 성능을 보장한다
  • 데이터의 분포에 영향을 덜 받는다

단점

• 임시 배열을 저장하기 위해 추가 공간이 필요하다 → 제자리 정렬 알고리즘 X
  • 메모리가 제한된 환경에는 적합하지 않으며, 작은 데이터 집합에는 효율적이지 않다

 

면접 질문

1. 합병 정렬에 대해서 설명해주세요
2. 합병 정렬의 시간복잡도에 대해서 설명해주세요

 

출처

https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

https://velog.io/@eddy_song/merge-sort

https://jinhyy.tistory.com/9

https://velog.io/@jimmy48/병합-정렬Merge-Sort

https://mfamcs.netlify.app/docs/algorithms/%EB%B3%91%ED%95%A9%20%EC%A0%95%EB%A0%AC