선택 정렬 (selection sort)

개념
- 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
- 오름차순을 기준으로 했을 때 리스트의 첫 번째 인덱스에는 해당 리스트에서의 최솟값을 찾아 치환하고 그 다음 인덱스에서는 첫번째 인덱스를 제외한 리스트에서의 최솟값을 찾아 치환하고를 반복해 나가는 방식
정렬 과정
- 주어진 배열 중에서 최솟값을 찾는다
- 그 값을 맨 앞에 위치한 값과 교체한다
- 맨 앞에 위치한 값이 최솟값이라면 패스한다
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다
- 하나의 원소만 남을 때까지 위의 1~3 과정을 반복한다
예제
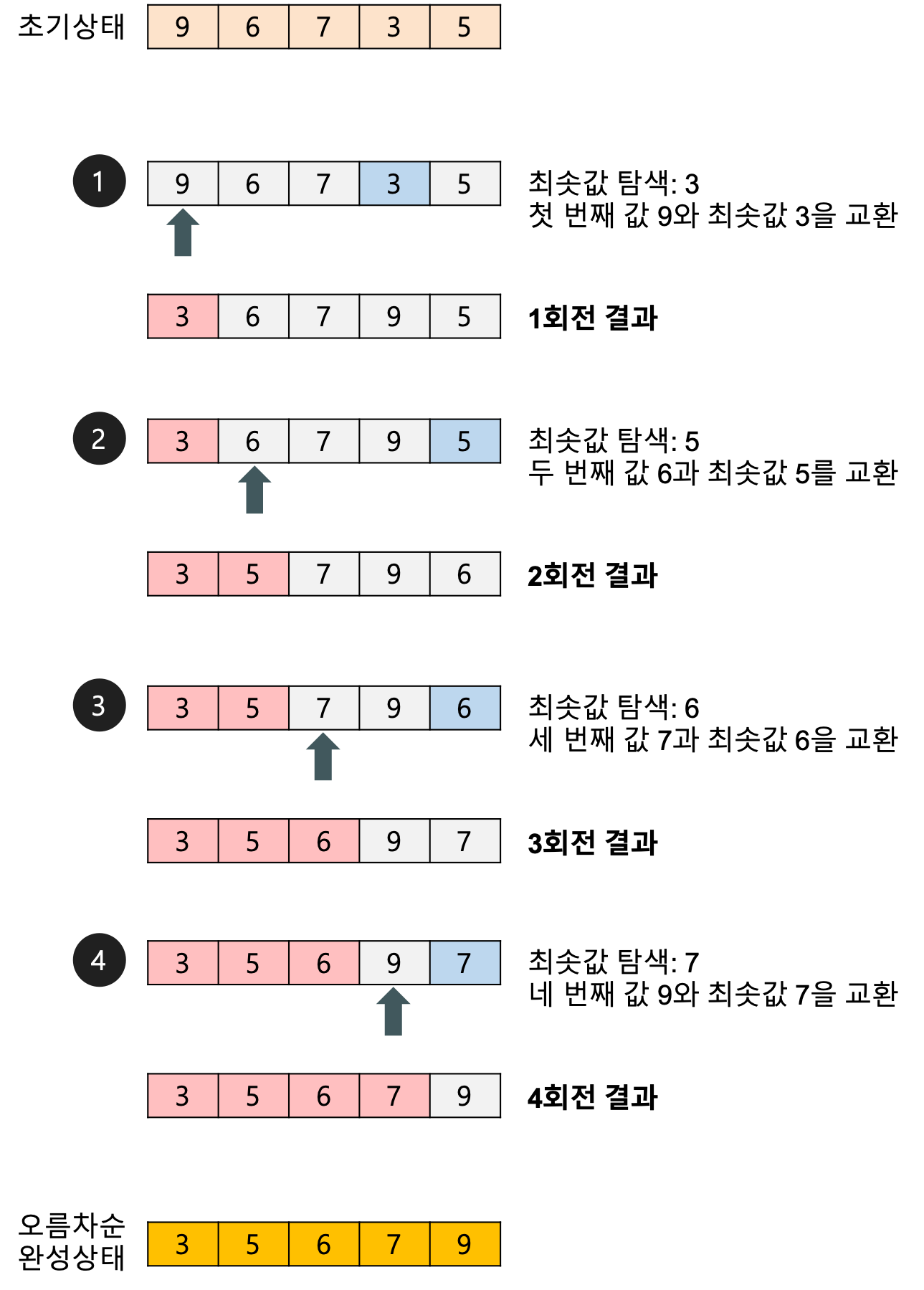
💡 배열에 9, 6, 7, 3, 5가 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해보자
1 회전
- 첫 번째 자료 9를 두 번째 자료부터 마지막 자료까지와 비교하여 가장 작은 값을 첫 번째 위치에 옮겨 놓는다.
- 이 과정에서 자료를 4번 비교한다.
2 회전
- 두 번째 자료 6을 세 번째 자료부터 마지막 자료까지와 비교하여 가장 작은 값을 두 번째 위치에 옮겨 놓는다.
- 이 과정에서 자료를 3번 비교한다.
3 회전
- 세 번째 자료 7을 네 번째 자료부터 마지막 자료까지와 비교하여 가장 작은 값을 세 번째 위치에 옮겨 놓는다.
- 이 과정에서 자료를 2번 비교한다.
4 회전
- 네 번째 자료 9와 마지막에 있는 7을 비교하여 서로 교환한다.
예제 코드 (코틀린)
fun selectionSort(arr: IntArray) {
// i : 최솟값을 고정할 자리의 인덱스
for(i in 0 until arr.size - 1) { // 마지막 값은 자동으로 정렬되기 때문에 (숫자 개수 - 1)만큼 반복
// minIndex : 최솟값의 인덱스
// 고정한 값을 제외한 값들 중에서 최솟값을 찾는다
var minIndex = i
for (j in i+1 until arr.size) {
if (arr[j] < arr[minIndex]) {
minIndex = j
}
}
// swap(arr[i], arr[minIndex])
if (i != minIndex) { // 이미 i에 최솟값이 들어있다면 swap하지 않는다
val tmp = arr[i]
arr[i] = arr[minIndex]
arr[minIndex] = tmp
}
}
//출력
arr.forEach {
print(it)
}
}시간복잡도
데이터가 n개일 때,
1회전에서의 비교 횟수 : 1 ~ n-1 ⇒ n-1개
2회전에서의 비교 횟수 : 2 ~ n-1 ⇒ n-2개
(n-1) + (n-2) + (n-3) + (n-4) +... + 3 + 2+ 1 = n(n-1)/2 => O(n^2)
공간복잡도
데이터가 n개일 때,
주어진 배열 안에서 교환을 통하여 정렬이 되므로,
O(n)
특징
- 데이터의 개수가 적을 때 좋은 성능을 보이지만, 데이터의 개수가 많아질수록 성능이 떨어진다.
장점
- 구현이 매우 간단하고, 소스 코드가 직관적이다
- 제자리 정렬(in-place sorting) 알고리즘 : 주어진 배열 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
- 내림차순으로 정렬되어있는 요소를 오름차순으로 재정렬할 때 효율이 좋다
- 비교 횟수는 많지만, 실제로 교환하는 횟수는 적다
- 교환이 많이 일어나는 자료 상태라면 효율적이다
단점
- 불안정 정렬 : 중복된 값이 있을 때 요소의 순서가 바뀔 수 있다
- 이미 정렬된 상태에서 소수의 자료를 추가한 후 재정렬을 하면 비효율적이다
- 시간 복잡도는 O(n^2)로, 대량의 데이터를 다루는데는 적합하지 않다
면접 예상 질문
- 선택 정렬에 대해 설명해주세요
- 버블 정렬이랑 선택 정렬의 차이점을 설명해주세요
참고 URL
https://notbusyperson.tistory.com/35
https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html